The 31st ASEAN Summit and its related meetings, including the East Asia Summit, start today and will run through 14 November. Lost in the hoopla over Trump’s attendance and the ongoing tension in the Korean peninsula is the critical agenda of ASEAN secretariat (ASEC) reform.

In August this year, the group’s foreign ministers simply noted that they were ‘pleased with the ongoing progress in the implementation of the recommendations by the High-Level Task Force (HLTF) on Strengthening the ASEAN Secretariat and Reviewing the ASEAN Organs’. With the annual tradition of parsing out ASEAN statements over China and the South China Sea, crucial intra-ASEAN plans have taken a backseat.

Yet, prompted by the infamous 2012 Cambodian chairmanship, the group formed the HLTF to boost ASEC’s role and capacity as an ‘institutional solution’. By the 2014 ASEAN Summit, regional leaders declared that they were committed to ‘strengthening ASEAN’s institutional capacity to support the ASEAN Community building, through streamlining and improving its work processes and coordination among ASEAN Organs and Bodies, enhancing the conduct of ASEAN’s external relations and strengthening the ASEAN Secretariat’.

The ASEC reform, in other words, was part of a wider range of institutional reform policies, from streamlining meetings to empowering the secretary general (see here and here). Most if not all of those recommendations, however, hinge on ASEC’s budgetary capacity.

The ASEC employs around 300 staff with a budget of about $20 million by 2016. The amount is miniscule considering the over 1,000 meetings it must organise annually. Some of the meetings should be aligned with the local host (ASEAN chair) each year, which raises the complexity and cost. As ASEAN chair for the 2017 summit season, the Philippines has organised 283 meetings at a cost of about $300 million (and possibly more given the security needs).

The current ASEC budget is unsustainable. According to the Asian Development Bank Institute, by 2030, the number of ASEC staff must increase to 1,620 with a budget of about $220 million (more than 12 times the current budget). Those projections are based on the need to handle numerous ASEC activities that have grown (and will continue to grow) to fulfil the mandates of the ASEAN charter.

The projected budget includes staff salary increases to attract the best and brightest. As it stands, on average, ASEAN salaries were only two-thirds of those of a comparable Jakarta-based UN agency. Any ASEAN-wide institutional reform policies therefore would be harder to pursue without significantly boosting the budget’s size and structure.

The current budget structure is based on the members’ equal contribution, per the ASEAN charter. This basically boils down to a negotiation over the lowest common denominator— finding the balance between what Singapore and Indonesia could afford with what Laos and Myanmar could contribute.

But if we read the charter carefully, there’s room for a reinterpretation. As Article 30 of the charter notes, ‘The operational budget of the ASEAN secretariat shall be met by ASEAN Member States through equal annual contributions which shall be remitted in a timely manner’ (emphasis mine). There’s nothing specific about the monetary equal value of those contributions. Much like UNCLOS prescribes an ‘equitable solution’ to maritime disputes, member states in this sense have (relative) space to interpret ‘equal contribution’.

I suggest a reinterpretation based on two options: either (A) equal share (percentage) of each country’s annual expenditure, or (B) equal share based on each country’s economic development conditions.

Let’s assume under the current format that each member contributes $2 million. That figure represents a small fraction of each member’s annual expenditure—from roughly 0.004% (Singapore) to 0.052% (Laos). In Option A, equality in proportion of expenditure means that each member must contribute an equal share of its annual expenditure. I propose an equal share of 0.02% of members’ national expenditure (see the table below). That option could get us roughly $93 million (or around half of what ASEC needs by 2030).



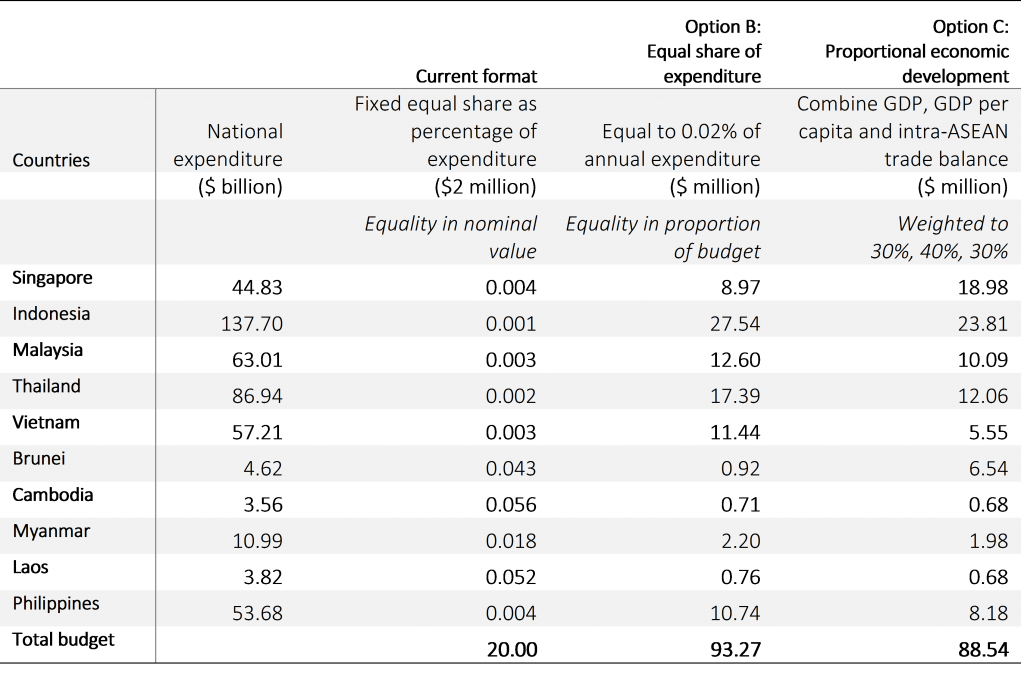
In Option B, equality in levels of economic development means that each member contributes ‘equally’ based on how developed its economy is. I propose that we use three different economic indicators: GDP, GDP per capita, and intra-ASEAN trade balance (each weighted differently: 30%, 40% and 30%, respectively). That option could get us to roughly $88 million (less than half of what ASEC needs by 2030).

Both options could be implemented gradually, perhaps within a three- to five-year scheme with a biannual review mechanism. If we can get to roughly the $100 million mark by 2025, then it would be a success. In any case, however, the problem with this reinterpretation idea will likely be political, especially if consensus decision-making remains.

Some members don’t want a strong secretariat, while others might simply be unwilling to pay more. After all, there remains a huge wealth gap within ASEAN, and changing the current equal monetary value format raises the ‘hierarchy of influence’ concerns. But if the challenges surrounding the South China Sea in recent years have taught us anything, isn’t it the case that the needs of the many outweigh the needs of the few?

The ideas in this post were presented at a workshop organised as part of the Australia–Singapore–United States Policy Trialogue on Southeast Asia (APTOS) hosted by the Daniel K. Inouye Asia-Pacific Center for Security Studies in Honolulu, Hawaii, on 25–27 October 2017.