Recent reporting that the search for missing Malaysian Airlines Flight 370 might be soon called off got me thinking about the methodology of search. For my sins, I spent time in operations research in my early days in Defence. It was back in the ‘Defence of Australia’ doctrine days, and our group was working with what’s now the Defence Science and Technology Group (DST Group) on a ‘wide area surveillance study’. Surveillance isn’t the same as search but in a slowly evolving situation they’re described by similar mathematics.
Search theory in its modern form goes back to WW2, when the theory was developed primarily for hunting submarines in the open ocean. The classic text on the subject is The Theory of Optimal Search. It’s maths heavy, but the bottom line is that searching is a science, and it’s possible to have a pretty good idea in advance what the likelihood of success is and what resources will be required for a given confidence level.
The technique that’s being used for the search for MH370 is called Bayesian search theory. (Trigger alert: sensitive readers prone to flashbacks about year 11 mathematics classes are warned of potentially disturbing content ahead.) The technique has been used to locate sunken vessels and missing aircraft in the past. Famous examples include a missing hydrogen bomb (!) that went into the Mediterranean after a B-52 crash and the USS Scorpion, a nuclear submarine that disappeared in the Atlantic in 1968. The story of the search for the Scorpion, as told in the book Blind Man’s Bluff (though the details are disputed), illustrates how the Bayesian technique works. More recently, the technique helped searchers locate the wreckage of Air France Flight 447 in the Southern Atlantic in 2009.
The ideas behind it are simple enough. First you collect as much information as possible about the circumstances that led to the object of the search being lost in the first place. That allows the construction of a probability map of the potential search area. The highest probability will be where the consensus of expert opinion places the location, which is where you start looking.
Before going into further detail, it’s worth thinking about how we intuitively search. When I misplace my glasses at home (only three times a day), I first look in the obvious places, like the coffee table or my desk. If I don’t find them, I search less obvious but still plausible places; on bookshelves, or in the bathroom. If I still don’t find them, I have to decide between looking in increasingly unlikely places and revisiting the most likely ones. Generally I’ll have another look around the coffee table long before I head for the garage to check under the lawn mower. That’s an implementation of Bayesian theory.
There are some subtleties if we want to quantify my search strategy. If I don’t find them on the coffee table, then it’s more likely that they’ll be on my desk than was the case before I started looking (because I’ve excluded one area). But since no search is 100% efficient, there’s still a probability that they’re on the coffee table and I just missed them—but the probability is smaller than it was before. After every search, I mentally update my estimate of probabilities for both searched and unsearched areas. The best strategy is to always search in the most likely area, even if I’ve already looked there.
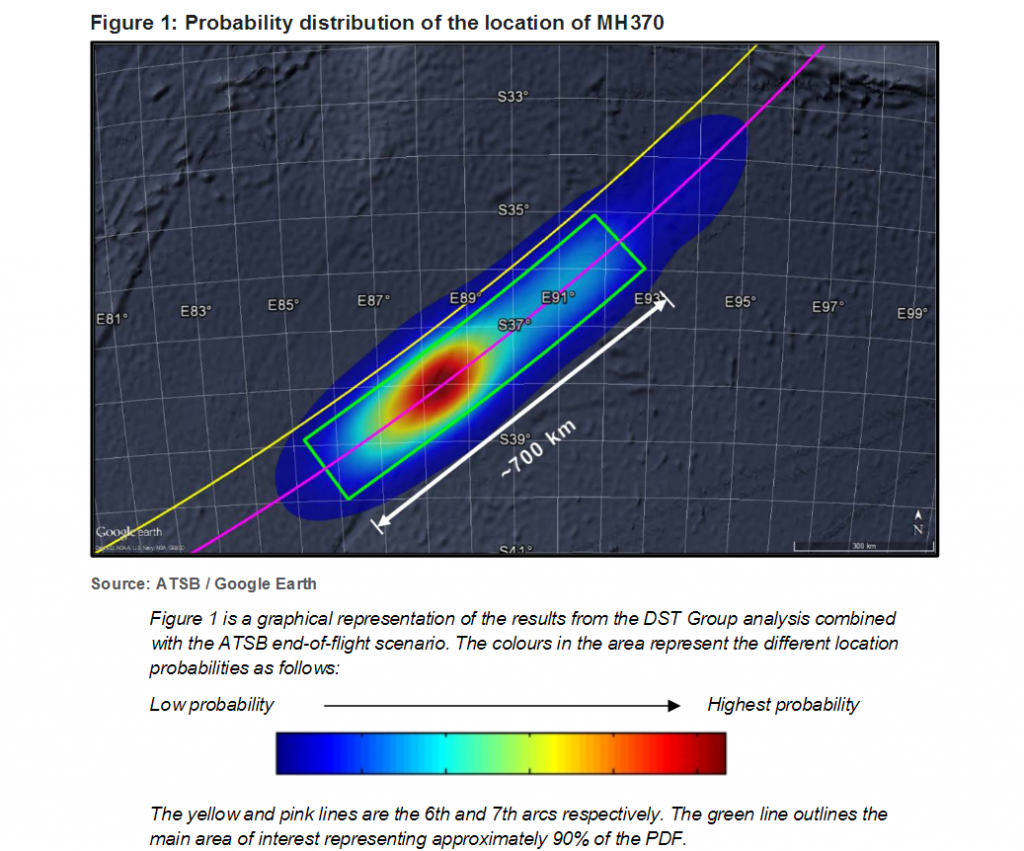
In the case of MH370, expert aviation advice and geolocational data of the aircraft from communications satellites allowed the DST Group to construct the initial probability map shown above. (The grisly details are here [pdf].) As the example above suggests, every time a location is searched, all of the probabilities need to be recalculated, so the map is only a snapshot in time.
Let’s put some indicative numbers in to see how it works. Let’s say that the original estimate of the wreckage being in an area was 20% and that the search equipment has an 80% chance of finding it if it’s there. Even after an unsuccessful search, there’s still a 4.7% chance that the wreckage is there, but happened to evade detection (which is probably what happened during the search for Air France Flight 447). A neighbouring area with an initial 10% probability estimate now has a 10.8% chance of containing the wreckage.
There’s a fair amount of public information regarding the search for MH370, and there are bloggers following and mapping the search. Recent searching is in the lower probability regions of the initial map, which isn’t surprising since the search has been going for over two years. Not knowing the search efficiency—the weather in the search area ensures that it’ll be well under 100%—it’s hard to tell what the optimum strategy is now, but it might well be worth having another look in the places initially judged most likely before giving up.

